در این مقاله به بررسی تاریخچه مثلثات در علم ریاضی میپردازیم. اما ابتدا این مقاله را با پرسش دو سوال از شما آغاز می کنیم؟
- تا کنون در خلوت خود به چگونگی پیدایش جهان هستی فکر کرده اید؟
- آیا تا کنون در ارتباط با چگونگی خلق انسان و موجودات روی زمین با دوستان خود گفت و گو کرده اید؟
تاریخ و منشا به وجود آمدن هر چیزی همیشه در زندگی آدمی دارای اهمیت بوده است و آگاهی از گذشته، نحوه پدید آمدن و آشنایی و کشف حقیقت در مورد گذشته برای بسیاری از افرادی که روحیه ماجراجو دارند جالب و قابل بحث می باشد. آگاهی از تاریخچه هر موضوع و رویدادی می تواند اطلاعات و نگرش شما را بالا برده و بینشی وسیع تر پیدا کنید. آگاهی از تاریخ علم نیز سبب کمک و یاری زیادی به انسان خواهد شد و باعث می شود تا دانش را از شبه دانش و درست را از نا درست راحت تر تشخیص دهد و گرفتار خرافات و یا اطلاعات اشتباه افراد دیگر نشود.
تاریخچه ریاضیات نیز برای علاقهمندان به علم ریاضیات، اساتید و دانش آموزان و محققان موضوعی جالب توجه بوده است و مثلثات یکی از مباحث شیرین و البته دشوار در ریاضیات است که ما امروز در این مقاله قصد داریم تا در حد توان شما را با تاریخچه مثلثات در ریاضی آشنا کنیم.
آشنایی با تاریخچه مثلثات
فهرست مطالب
- آشنایی با تاریخچه مثلثات
- ارتباط میان اخترشناسی و پیدایش مثلثات:
- نخستین گام اصلی در پیدایش مثلثات تا پیدایش پیچیده ترین دستورهای مثلثاتی:
- خواجه نصیرالدین طوسی و جمع بندی یافته های مثلثاتی:
- اثبات ایرانی بودن علم مثلثات
- ریشه واژه جیب (سینوس) و دلیل استفاده از آن:
- آشنایی مقدماتی با تابع مثلثاتی:
- تعریف روی مثلث قائم الزاویه:
- تعریف کسینوس یک زاویه:
- تعریف تانژانت یک زاویه:
- تعریف کتانژانت یک زاویه:
- تعریف کسکانت یک زاویه:
- تعریف سکانت یک زاویه:
- آشنایی با نسبت های مثلثاتی در روی دایره مثلثاتی
با شنیدن نام مثلثات اولین چیزی که به ذهنتان می رسد چیست؟
همانطور که از اسم مثلثات نیز پیداست در ابتدا این موضوع که این شاخه از ریاضیات ممکن است مربوط به مثلث بوده باشد و یا ارتباط با مسائل مثلثی را دارا باشد به ذهنتان خواهد رسید. لغت مثلثات از مثلث گرفته شده است و ترجمه لغت فرانسوی هم ارز که به معنای “اندازه گیری مثلث” می باشد است. مثلثات در زبان انگلیسی Trigonometry نامیده می شود و در فارسی نیز معادل در نظر گرفته شده برای این واژه “سه بروارگان” می باشد.
ارتباط میان اخترشناسی و پیدایش مثلثات:
در اختر شناسی برای تعیین موقعیت ستارگان و تعیین جای آن ها و هم چنین فاصله میان دو ستاره و سایر اطلاعات مرتبط به آنها اخترشناسان به عدد نیاز داشتهاند. در آن زمان، وسایل امروزی مانند تلسکوپ، ابزارهای اندازه گیری و… وجود نداشت. بنابراین ستارهشناسانی مانند خیام، به کمک روابط هندسی توانستند به محاسبات خارق العاده ای بدون ابزارهای محاسباتی دست یابند.
اختر شناسان در اخترشناسی برای حل مسائلی که با آن ها مواجه می شوند به مثلثات نیاز دارند. یکی از ساده ترین این مسائل پیدا کردن یک کمان دایره بر حسب درجه با آگاهی از شعاع دایره و طول وتر این کمان می باشد (و یا برعکس). همانطور که می دانید سینوس یک کمان از لحاظ قدرمطلق مساوی با نصف طول دو برابر آن کمان است و همین یک جمله اساس و پایه بین کمان ها و وترها را در دایره تشکیل می دهد و شروع مثلثات نیز به همین بخش ها بر می گردد.
هیپارک یکی از اخترشناسان سده دوم میلادی است که یکی از قدیمی ترین جدول هایی که طول برخی از کمان ها در آن نوشته شده است متعلق به این شخص می باشد؛ تنظیم این جدول سبب نخستین گام و البته گامی کوچک برای پیدایش مثلثات می باشد.
منه لائوس که یکی از ریاضیدانان و بطلمیوس که یکی از اختر شناسان می باشد و هر دو همانند هیپارک متعلق به سده دوم میلادی هستند در این زمینه آثار و نوشته هایی را از خود باقی گذاشتهاند اما لازم به ذکر است که تمامی کارهای اخترشناسان و ریاضیدانان در حوزه هندسه بوده و به مفاهیم اصلی مثلثات دست نیافتهاند.
نخستین گام اصلی در پیدایش مثلثات تا پیدایش پیچیده ترین دستورهای مثلثاتی:
آریابهاتا که یکی از ریاضیدانان سده پنجم میلادی می باشد تعریفی برای نیم وتر یک کمان-یعنی همان سینوس ارائه داد و سبب نخستین گام اصلی در پیدایش مثلثات شد. از آن پس سایر فعالیت ها کارهایی که در حوزه شکل گیری مثلثات صورت گرفت توسط دانشمندان ایرانی انجام شد. تنظیم اولین جدول سینوسی توسط خوارزمی صورت گرفت بعد از او دانشمندان بسیاری برای تکمیل کردن این جدل و سایر مفاهیم موجود در مثلثات تلاش کردند.
شخصی به نام کروزی به دلیل نیازهای موجود در اخترشناسی برای اولین بار مفهوم تانژانت را تعریف کرد که البته تانژانت در آن زمان “ظلل” نامیده می شد و پس از این افراد “ابوریحان بیرونی” و “ابوالوفای بوزجانی” تلاش های زیادی در این حوزه انجام دادند موفق به پیدایش پیچیده ترین دستورهای مثلثاتی شدند و همچنین جدول های سینوسی-تانژانتی را با دقت بالاتری تنظیم کردند.
خواجه نصیرالدین طوسی و جمع بندی یافته های مثلثاتی:
پس از توضیحاتی که در بخش قبل داده شد و پس از تلاش تمامی دانشمندان نام برده شده در نهایت خواجه نصیرالدین طوسی به جمع بندی تمام کارهای دانشمندان ایرانی پیش از خود پرداخت و کتاب مستقل مثلثات را نوشت. غیاث الدین جمشید کاشانی که یکی از ریاضیدانان زمان تیموریان بوده است با روش زیبا و خاصی که برای حل معادلات درجه دوم پیدا کرده بود پس از خواجه نصیر الدین طوسی موفق شد تا راهی برای محاسبه سینوس کمان یک درجه با هر دقت دلخواهی را پیدا کند.
دانش مثلثات از سده پانزدهم میلادی در اروپای غربی پیشرفت های بعدی خود را آغاز کرد.
اثبات ایرانی بودن علم مثلثات
یکی از مواردی که تا حدودی ایرانی بودن این دانش را نشان می دهد این است که: ریاضی دانان ایرانی برای سینوس از واژه ای به نام “جیب” (واژه عربی به معنای گریبان) و برای کسینوس از واژه “جیب تمام” استفاده می کردند. زمانی که نوشته های این ریاضی دانان به ویژه خوارزمی به زبان لاتین و اروپایی ترجمه گردید واژه سینوس را جایگزین واژه جیب کردند.
ریشه واژه جیب (سینوس) و دلیل استفاده از آن:
فزازی یک ریاضیدان ایرانی بود که اولین کتابی را که به دستور خلیفه عباسی ترجمه کرد کتابی در حوزه اخترشناسی و از نوشته دانشمندان هندی بود. در این نوشته از واژه ای به نام “جیا” استفاده شده بوده است. جیا در زبان سانسکریت به معنای وتر و گاهی نیز “نیم وتر” می باشد و مترجم برای احترام گذاشتن به اثر و نویسندگان کتاب این واژه را تغییر نمی دهد.
با توجه به این که “جیا” در زبان عربی معنای خاصی ندارد این واژه را به کلمه جیب تبدیل می کند. دیدگاه دیگر و منطقی تری برای این تبدیل وجود دارد و آن هم این است که در ترجمه از واژه جیب بر وزن سیب استفاده شد که معنای آن ” تکه چوب عمود” یا “دیرک” است.
همانطور که گقته شد نام واژگان مثلثات در گذشته با امروز تفاوت هایی را داشته است که جدول زیر نشان دهنده این تغییرات اسمی می باشد:
| نام قدیم در فارسی | معنای نام | نام امروزی |
| جیب | گریبان | سینوس |
| جیب تمام | گریبان پر | کسینوس |
| ظل،ظل معکوس | سایه | تانژانت |
| ظل تمام،ظل مستوی | سایه پُر | کتانژانت |
| قاطع،قطر ظل | بُرنده | سکانت |
| قاطع تمام | بُرنده پُر | کسکانت |
آشنایی مقدماتی با تابع مثلثاتی:
تا اینجا در این مقاله سرگذشت و تاریخچه و چگونگی به وجود آمدن مثلثات را در حد توان برای شما توضیح دادیم و اکنون در گام بعدی برای آمادگی ذهن شما و تکمیل نوشته ها قصد داریم تا به صورت سطحی شما را با مثلثات آشنا کنیم و در مقالات و کلیپ های بعدی این شاخه از ریاضیات را موشکافانه بررسی کنیم.
مثلثات در واقع مطالعه اندازه گیری زاویه می باشد اما نباید این موضوع را با اندازه گیری مقدماتی زاویه در هندسه یکی دانست و این بدان معنا نیست و مثلثات در حقیقت محاسبه با توابع خاصی است که به زوایا بستگی دارند و به علت کارد آن ها در مثلثات “توابع مثلثاتی” نامیده می شوند.
تعریف روی مثلث قائم الزاویه:
ما برای تعریف توابع مثلثاتی از یک مثلث قائم الزاویه که قطعا همگی آن را می شناسید استفاده می کنیم.
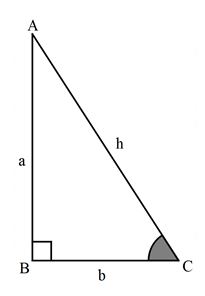
مثلث قائم الزاویه زیر را در نظر بگیرید:
- به ضلغ روبروی زاویه قائمه که بلندترین ضلع مثلث نیز می باشد وتر گفته می شود که در این شکل با حرف لاتین h نمایش داده ایم.
- ضلع مقابل به وتر را با حرف لاتین a نمایش داده ایم.
- ضلع مجاور به زاویه قائمه را با حرف لاتین b نشان داده ایم.
اکنون می خواهیم توابع مثلثاتی را برای زاویه c روی مثلث ABC تعریف نماییم.
تعریف سینوس یک زاویه:
نسبت ضلع مقابل زاویه تقسیم بر وتر را سینوس (sin) می گویند که با توجه به شکل یعنی: sin(c)=a/h
تعریف کسینوس یک زاویه:
نسبت ضلع مجاور به وتر را کسینوس (cos) می گویند که با توجه به شکل یعنی: cos(c)=b/h
تعریف تانژانت یک زاویه:
نسبت ضلع مقابل به مجاور را تانژانت (tangent) می گویند که با توجه به شکل یعنی: tan(c)=a/b
تعریف کتانژانت یک زاویه:
نسبت ضلع مجاور به ضلع مقابل زاویه را (cotangent) می گویند که با توجه به شکل یعنی:cot(c)=b/a
تعریف کسکانت یک زاویه:
نسبت وتر به ضلع مقابل زاویه را (cosecant) می گویند (این مقدار را می توان از معکوس کردن نسبت مثلثاتی سینوس نیز یافت) که با توجه به شکل یعنی:
csc(c)=1/sin(c)=h/a
تعریف سکانت یک زاویه:
نسبت وتر به ضلع مجاور را (secant) می گویند که با توجه به شکل یعنی:
sec(c)=1/cos(c)=h/b
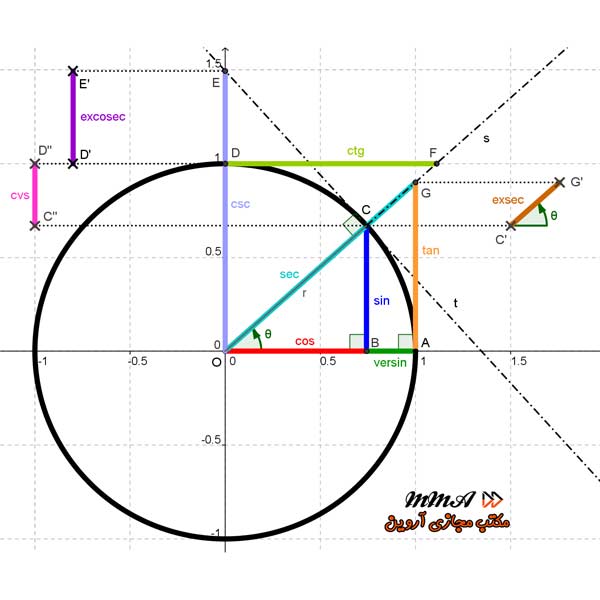
آشنایی با نسبت های مثلثاتی در روی دایره مثلثاتی
قطعا همگی نام دایره مثلثاتی را شنیده اید که این دایره دارای شعاع واحد است.
- مرکز این دایره روی نقطه مرکز مختصات دکارتی قرار گرفته است در نتیجه مختصات این نقطه می باشد.
- محور عمودی در این دایره سینوس (Sin) می باشد.
- محور افقی در دایره مثلثاتی کسینوس (Cos) نامیده می شود.
در مقالات بعدی ریاضی ما و دی وی دی های آموزشی مثلثات را از صفر تا صد آموزش خواهید دید.





?